微分方程数值解

为 ODE 和 PDE 求解器创建或修改 options 结构体

options = odeset(Name,Value,...) 创建 options 结构体，可以将其作为参数传递给 ODE 和 PDE 求解器。在结构体 options 中，指定选项具有指定的值。任何未指定的选项都使用默认值。例如，options = odeset('RelTol',1e-3) 返回 RelTol 设置为 1e-3 的 options 结构体。

options = odeset(oldopts,Name,Value,...) 使用新指定的名称-值对组修改现有的 options 结构体 oldopts。这样将覆盖指定选项的任何旧值，并将新选项的值添加到结构体中。

options = odeset(oldopts,newopts) 通过合并现有 options 结构体 oldopts 和新 options 结构体 newopts 来修改现有 options 结构体。任何不等于 [] 的新选项都会覆盖 oldopts 中的相应选项。

求解非刚性微分方程_低阶ode23()

[t,y] = ode23(odefun,tspan,y0)（其中 tspan = [t0 tf]）求微分方程组 \(y′=f(t,y)\) 从 t0 到 tf 的积分，初始条件为 y0。解 数组 y 中的每一行都与列向量 t 中返回的值相对应。

[t,y] = ode23(odefun,tspan,y0,options) 还使用由 options（使用 odeset 函数创建的参数）定义的积分设置。例如，使用 AbsTol 和 RelTol 选项指定绝对误差容限和相对误差容限，或者使用 Mass 选项提供质量矩阵。

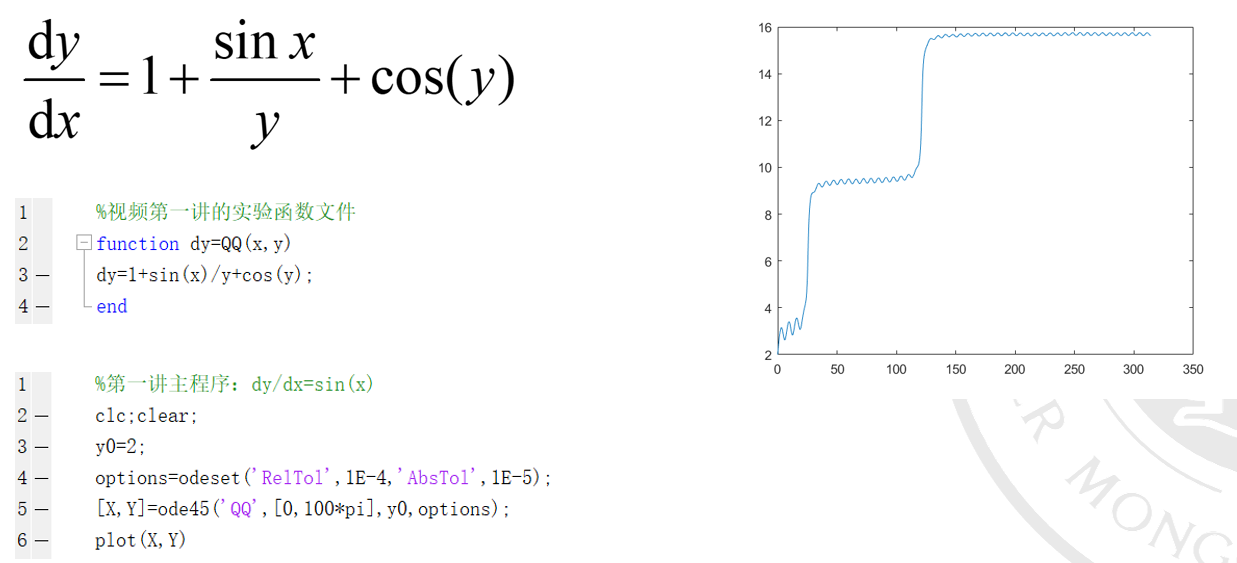
这是一个简单的求解实例，plot(X,Y)可以直接绘制原方程图形：

这是一个微分方程组示例：

求解高阶微分方程，像下面这样：

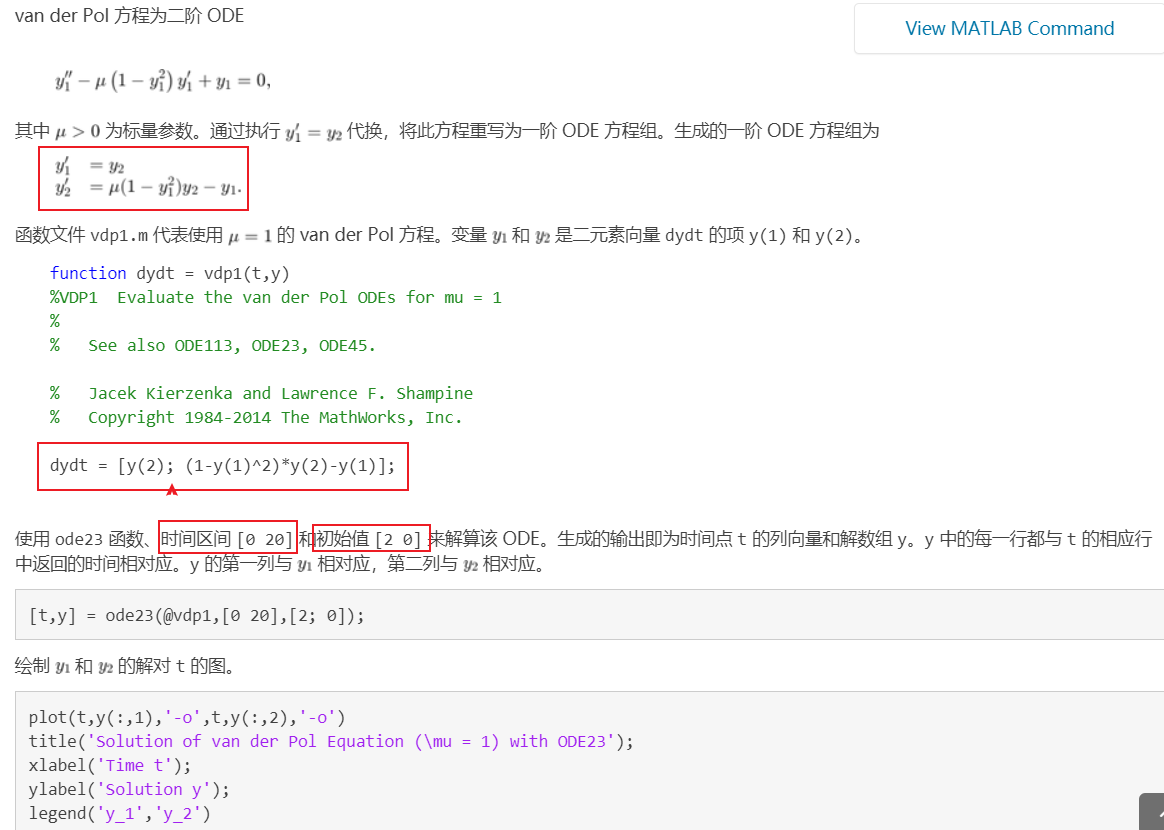
在上述例子中， ode23() 函数的 odefun 参数写成 'funname' 或 @funname两种形式都可以； 微分方程组的ode_function中y(1)=...; y(2)=...; 或y=[...; ...]; 两种形式都可以。 另外需要注意： 解出来的 数组 y 中的每一行都与列向量 t 中返回的值相对应。解高阶微分方程时，y(:,1)(即y的第一列) 对应是y' 的解；y(:,2)对应的是y'' 的解。

求解非刚性微分方程_中阶ode45()

基本使用与ode23() 完全一致。

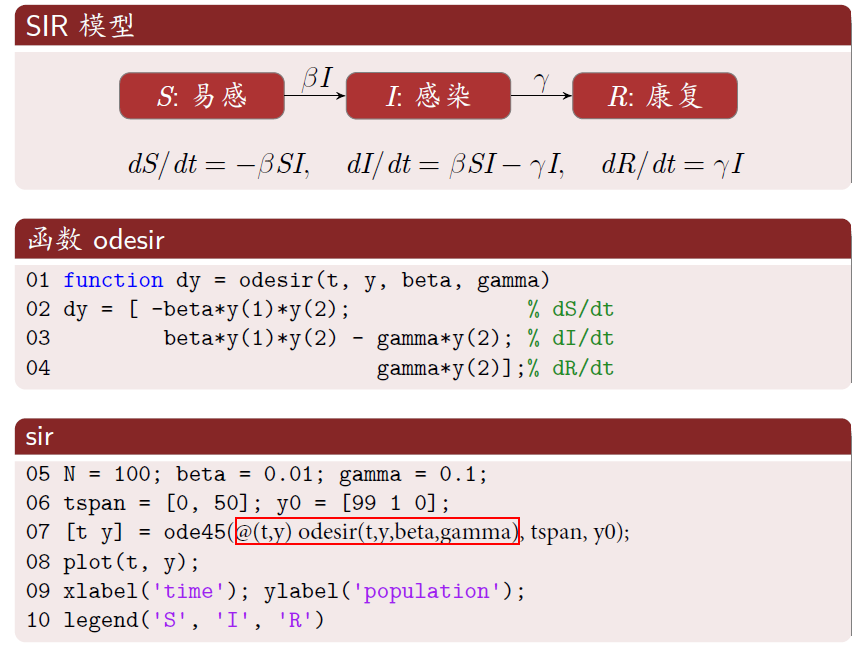
要编写带有时变项的ode，将时变项作为函数参数，在ode45() 的odefun参数中把函数句柄写成如下这种形式： 这是一个经典SIR模型